2 Đề kiểm tra 1 tiết chương 1 môn Giải tích 12 - Năm học 2016-2017 - Trường THPT Nguyễn Văn Cừ (Có đáp án)

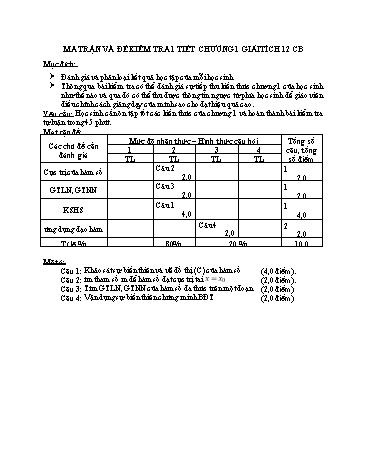
 MA TRẬN VÀ ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 1 GIẢI TÍCH 12 CB
Mục đích: 
 ➢ Đánh giá và phân loại kết quả học tập của mỗi học sinh 
 ➢ Thông qua bài kiểm tra có thể đánh giá sự tiếp thu kiến thức chương 1 của học sinh 
 như thế nào và qua đó có thể thu được thông tin ngược từ phía học sinh để giáo viên 
 điều chỉnh cách giảng dạy của mình sao cho đạt hiệu quả cao.
Yêu cầu: Học sinh cần ôn tập tốt các kiến thức của chương 1 và hoàn thành bài kiểm tra 
tự luận trong 45 phút.
Ma trận đề:
 Mức độ nhận thức – Hình thức câu hỏi Tổng số 
 Các chủ đề cần 
 1 2 3 4 câu, tổng 
 đánh giá
 TL TL TL TL số điểm
 Câu 2 1
 Cực trị của hàm số
 2,0 2,0
 Câu 3 1
 GTLN, GTNN
 2,0 2,0
 Câu 1 1
 KSHS
 4,0 4,0
 Câu 4 2
 ứng dụng đạo hàm
 2,0 2,0
 Tỉ lệ % 80% 20 % 10,0
Mô tả: 
 Câu 1: Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (4,0 điểm).
 Câu 2: ìm tham số m để hàm số đạt cực trị tai = 0 (2,0 điểm).
 Câu 3: Tìm GTLN, GTNN của hàm số đa thức trên một đoạn (2,0 điểm)
 Câu 4: Vận dụng sự biến thiên chứng minh BĐT (2,0 điểm) Trường THPT Nguyễn Văn Cừ KIỂM TRA MỘT TIẾT GIẢI TÍCH 12
 Tổ Toán Tin TD-QPAN Chương I, Năm học 2016 – 2017 
 ——————— Thời gian làm bài: 45 phút, không kể giao đề 
Đề số 02
Câu 1 (4,0 điểm): Khảo sát sự biến thiên vẽ đồ thị hàm số = 4 ―2 2 ―1
Câu 2 (2,0 điểm): Xác định m để hàm số = 3 ―( + 1) 2 +3 + 1 đạt cực 
tiểu tại = 1
Câu 3 (2,0 điểm): Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
 = 3 +3 2 ―9 + 10 trên [ ― 2;2]
 x2
Câu 4 (2,0 điểm): Chứng minh rằng x 0 :1 cos x
 2
 —————– Hết—————–
 Thí sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì thêm.
 Họ và tên học sinh: ......................................; Lớp: ...................... 3 Hàm số = 3 ―3 2 ―9 + 5 liên tục trên đoạn [ ― 2;2] 0,25
 ′ = 3 2 ― 6 ― 9 0,25
 x 1
 2 
 ′ = 0 3x 6x 9 0 0,5
 x 3  2;2
 ( ―1) = 10; ( ―2) = 3; (2) = ―17 0,5
 Vậy maxy 10 tại = ―1; miny 17 tại = 2
  2;2  2;2 0,5
4 2
 Xét hàm số ( ) = 1 ― 2 ― cos , > 0
 Ta có: ′( ) = ― + sin , > 0 0,25
 ′′( ) = ―1 + cos ≤ 0, ∀ .0 0,25
 ⇒ ′( ) nghịch biến trên (0; + ∞) ⇒ ′( ) 0 0,5
 ⇒ ( ) nghịch biến trên (0; + ∞) ⇒ ( ) 0 0,5
 2 2
 0,5
 Hay 1 ― 2 ― cos 0 ⇔1 ― 2 0 3 Hàm số = 3 +3 2 ―9 + 10 liên tục trên đoạn [ ― 2;2] 0,25
 ′ = 3 2 + 6 ― 9 0,25
 x 1
 2 
 ′ = 0 3x 6x 9 0 0,5
 x 3  2;2
 (1) = 5; ( ―2) = 32; (2) = 12 0,5
 Vậy maxy 32 tại = ―2; miny 5 tại = 1
  2;2  2;2 0,5
4 2
 Xét hàm số ( ) = 1 ― 2 ― cos , > 0
 Ta có: ′( ) = ― + sin , > 0 0,25
 ′′( ) = ―1 + cos ≤ 0, ∀ .0 0,25
 ⇒ ′( ) nghịch biến trên (0; + ∞) ⇒ ′( ) 0 0,5
 ⇒ ( ) nghịch biến trên (0; + ∞) ⇒ ( ) 0 0,5
 2 2
 0,5
 Hay 1 ― 2 ― cos 0 ⇔1 ― 2 0