4 Đề kiểm tra học kì I môn Toán 11 - Trường THPT Krông Ana (Có đáp án)

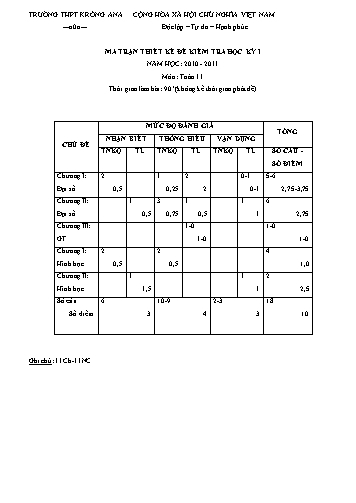
 TRƯỜNG THPT KRÔNG ANA CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM
 ---o0o--- Độc lập – Tự do – Hạnh phúc
 MA TRẬN THIẾT KẾ ĐỀ KIỂM TRA HỌC KỲ I
 NĂM HỌC: 2010 - 2011
 Môn: Toán 11
 Thời gian làm bài: 90’ (không kể thời gian phát đề)
 MỨC ĐỘ ĐÁNH GIÁ
 TỔNG
 NHẬN BIẾT THÔNG HIỂU VẬN DỤNG
 CHỦ ĐỀ
 TNKQ TL TNKQ TL TNKQ TL SỐ CÂU - 
 SỐ ĐIỂM
 Chương I: 2 1 2 0-1 5-6
 Đại số 0,5 0,25 2 0-1 2,75-3,75
 Chương II: 1 3 1 1 6
 Đại số 0,5 0,75 0,5 1 2,75
 Chương III: 1-0 1-0
 GT 1-0 1-0
 Chương I: 2 2 4
 Hình học 0,5 0,5 1,0
 Chương II: 1 1 2
 Hình học 1,5 1 2,5
 Số câu 6 10-9 2-3 18
 Số điểm 3 4 3 10
Ghi chú: 11Ch-11NC II) TRẮC NGHIỆM TỰ LUẬN
Câu 11 (2 điểm) Giải các phương trình sau: 
a) 2sin2 x 5cos x 1 0 b)sin 2x 3 cos 2x 2
Câu 12 (2,5 điểm) Cho hình chóp S. ABCD có đáy là hình bình hành.
 a) Chứng minh đường thẳng AB song song với mặt phẳng (SCD).
 b) Xác định giao tuyến của các cặp mặt phẳng (SAB) và (SCD), (SAC) và (SBD).
 c) Gọi G là trọng tâm tam giác SBC, xác định thiết diện cắt hình chóp bởi mặt phẳng (BGD). Chứng 
 minh đường thẳng SA song song với mặt phẳng (BGD).
PHẦN RIÊNG (3 điểm)
Học sinh học theo chương trình nào chỉ được làm phần đề theo chương trình đó.
A) Theo chương trình chuẩn
 u7 u2 15
Câu 13A) (1 điểm) Cho cấp số cộng (un ) thỏa mãn: 
 u4 u6 20
 a) Tìm số hạng đầu u1 và công sai d của cấp số cộng trên.
 b) Tìm n sao cho Sn 115 .
 3 1
Câu 14A) (1 điểm) Tìm x bi ết: C x 5C x
Câu 15A) (1 điểm) Có 14 người gồm 8 nam và 6 nữ, xét phép thử “Chọn ngẫu nhiên một tổ 6 người từ 14 
 người trên”. 
 a) Tính n  của phép thử trên.
 b) Tính xác suất để chọn được một tổ gồm toàn nam.
 c) Tính xác suất để chọn được một tổ có ít nhất là một nữ.
B) Theo chương trình nâng cao 
Câu 13B (1 điểm) Trên giá sách có 4 quyển sách Toán, 3 quyển sách Vật lý và 5 quyển sách Hoá học khác 
nhau. Lấy ngẫu nhiên 3 quyển sách. Gọi X là số quyển sách Toán lấy được.
a) Lập bảng phân bố xác suất của X.
b) Tính kì vọng của biến X.
 7
Câu 14B) (1 điểm) Tìm x biết : C1 C 2 C 3 x
 x x x 2
Câu 15B) (1 điểm) Giải phương trình 3 sin 5x cos5x 3 cos 2x sin 2x 0
 k
Ghi chú: n  :số phần tử của không gian mẫu; Cn : số các tổ hợp chập k của n phần tử, Sn=u1+u2+...+un
 BÀI LÀM
 BẢNG TRẢ LỜI TRẮC NGHIỆM II) TRẮC NGHIỆM TỰ LUẬN
Câu 11 (2 điểm) Giải các phương trình sau: 
a) 2sin2 x 5cos x 1 0 b)sin 2x 3 cos 2x 2
Câu 12 (2,5 điểm) Cho hình chóp S. ABCD có đáy là hình bình hành.
 a) Chứng minh đường thẳng AB song song với mặt phẳng (SCD).
 b) Xác định giao tuyến của các cặp mặt phẳng (SAB) và (SCD), (SAC) và (SBD).
 c) Gọi G là trọng tâm tam giác SBC, xác định thiết diện cắt hình chóp bởi mặt phẳng (BGD). Chứng 
 minh đường thẳng SA song song với mặt phẳng (BGD).
PHẦN RIÊNG (3 điểm)
Học sinh học theo chương trình nào chỉ được làm phần đề theo chương trình đó.
A) Theo chương trình chuẩn
 u7 u2 15
Câu 13A) (1 điểm) Cho cấp số cộng (un ) thỏa mãn: 
 u4 u6 20
 a) Tìm số hạng đầu u1 và công sai d của cấp số cộng trên.
 b) Tìm n sao cho Sn 115 .
 3 1
Câu 14A) (1 điểm) Tìm x bi ết: C x 5C x
Câu 15A) (1 điểm) Có 14 người gồm 8 nam và 6 nữ, xét phép thử “Chọn ngẫu nhiên một tổ 6 người từ 14 
 người trên”. 
 a) Tính n  của phép thử trên.
 b) Tính xác suất để chọn được một tổ gồm toàn nam.
 c) Tính xác suất để chọn được một tổ có ít nhất là một nữ.
B) Theo chương trình nâng cao 
Câu 13B (1 điểm) Trên giá sách có 4 quyển sách Toán, 3 quyển sách Vật lý và 5 quyển sách Hoá học khác 
nhau. Lấy ngẫu nhiên 3 quyển sách. Gọi X là số quyển sách Toán lấy được.
a) Lập bảng phân bố xác suất của X.
b) Tính kì vọng của biến X.
 7
Câu 14B) (1 điểm) Tìm x biết : C1 C 2 C 3 x
 x x x 2
Câu 15B) (1 điểm) Giải phương trình 3 sin 5x cos5x 3 cos 2x sin 2x 0
 k
Ghi chú: n  :số phần tử của không gian mẫu; Cn : số các tổ hợp chập k của n phần tử, Sn=u1+u2+...+un
 BÀI LÀM
 BẢNG TRẢ LỜI TRẮC NGHIỆM II) TRẮC NGHIỆM TỰ LUẬN
Câu 11 (2 điểm) Giải các phương trình sau: 
a) 2sin2 x 5cos x 1 0 b)sin 2x 3 cos 2x 2
Câu 12 (2,5 điểm) Cho hình chóp S. ABCD có đáy là hình bình hành.
 a) Chứng minh đường thẳng AB song song với mặt phẳng (SCD).
 b) Xác định giao tuyến của các cặp mặt phẳng (SAB) và (SCD), (SAC) và (SBD).
 c) Gọi G là trọng tâm tam giác SBC, xác định thiết diện cắt hình chóp bởi mặt phẳng (BGD). Chứng 
 minh đường thẳng SA song song với mặt phẳng (BGD).
PHẦN RIÊNG (3 điểm)
Học sinh học theo chương trình nào chỉ được làm phần đề theo chương trình đó.
A) Theo chương trình chuẩn
 u7 u2 15
Câu 13A) (1 điểm) Cho cấp số cộng (un ) thỏa mãn: 
 u4 u6 20
 a) Tìm số hạng đầu u1 và công sai d của cấp số cộng trên.
 b) Tìm n sao cho Sn 115 .
 3 1
Câu 14A) (1 điểm) Tìm x bi ết: C x 5C x
Câu 15A) (1 điểm) Có 14 người gồm 8 nam và 6 nữ, xét phép thử “Chọn ngẫu nhiên một tổ 6 người từ 14 
 người trên”. 
 a) Tính n  của phép thử trên.
 b) Tính xác suất để chọn được một tổ gồm toàn nam.
 c) Tính xác suất để chọn được một tổ có ít nhất là một nữ.
B) Theo chương trình nâng cao 
Câu 13B (1 điểm) Trên giá sách có 4 quyển sách Toán, 3 quyển sách Vật lý và 5 quyển sách Hoá học khác 
nhau. Lấy ngẫu nhiên 3 quyển sách. Gọi X là số quyển sách Toán lấy được.
a) Lập bảng phân bố xác suất của X.
b) Tính kì vọng của biến X.
 7
Câu 14B) (1 điểm) Tìm x biết : C1 C 2 C 3 x
 x x x 2
Câu 15B) (1 điểm) Giải phương trình 3 sin 5x cos5x 3 cos 2x sin 2x 0
 k
Ghi chú: n  :số phần tử của không gian mẫu; Cn : số các tổ hợp chập k của n phần tử, Sn=u1+u2+...+un
 BÀI LÀM
 BẢNG TRẢ LỜI TRẮC NGHIỆM II) TRẮC NGHIỆM TỰ LUẬN
Câu 11 (2 điểm) Giải các phương trình sau: 
a) 2sin2 x 5cos x 1 0 b)sin 2x 3 cos 2x 2
Câu 12 (2,5 điểm) Cho hình chóp S. ABCD có đáy là hình bình hành.
 a) Chứng minh đường thẳng AB song song với mặt phẳng (SCD).
 b) Xác định giao tuyến của các cặp mặt phẳng (SAB) và (SCD), (SAC) và (SBD).
 c) Gọi G là trọng tâm tam giác SBC, xác định thiết diện cắt hình chóp bởi mặt phẳng (BGD). Chứng 
 minh đường thẳng SA song song với mặt phẳng (BGD).
PHẦN RIÊNG (3 điểm)
Học sinh học theo chương trình nào chỉ được làm phần đề theo chương trình đó.
A) Theo chương trình chuẩn
 u7 u2 15
Câu 13A) (1 điểm) Cho cấp số cộng (un ) thỏa mãn: 
 u4 u6 20
 a) Tìm số hạng đầu u1 và công sai d của cấp số cộng trên.
 b) Tìm n sao cho Sn 115 .
 3 1
Câu 14A) (1 điểm) Tìm x bi ết: C x 5C x
Câu 15A) (1 điểm) Có 14 người gồm 8 nam và 6 nữ, xét phép thử “Chọn ngẫu nhiên một tổ 6 người từ 14 
 người trên”. 
 a) Tính n  của phép thử trên.
 b) Tính xác suất để chọn được một tổ gồm toàn nam.
 c) Tính xác suất để chọn được một tổ có ít nhất là một nữ.
B) Theo chương trình nâng cao 
Câu 13B (1 điểm) Trên giá sách có 4 quyển sách Toán, 3 quyển sách Vật lý và 5 quyển sách Hoá học khác 
nhau. Lấy ngẫu nhiên 3 quyển sách. Gọi X là số quyển sách Toán lấy được.
a) Lập bảng phân bố xác suất của X.
b) Tính kì vọng của biến X.
 7
Câu 14B) (1 điểm) Tìm x biết : C1 C 2 C 3 x
 x x x 2
Câu 15B) (1 điểm) Giải phương trình 3 sin 5x cos5x 3 cos 2x sin 2x 0
 k
Ghi chú: n  :số phần tử của không gian mẫu; Cn : số các tổ hợp chập k của n phần tử, Sn=u1+u2+...+un
 BÀI LÀM
 BẢNG TRẢ LỜI TRẮC NGHIỆM MÃ ĐỀ 153
 1 2 3 4 5 6 7 8 9 10
A X X X
B X X
C X X X
D X X
 MÃ ĐỀ 237
 1 2 3 4 5 6 7 8 9 10
A X X
B X X X
C X X X
D X X
 MÃ ĐỀ 210
 1 2 3 4 5 6 7 8 9 10
A X X X X
B X X
C X X
D X X Gọi I AM  BD , ta có VIBM đồng dạng VIDA suy ra IM: 0,25
 IA = BM: DA = 1: 2.
 Từ đó suy ra MI: MA = 1: 3 = MG: MS nên SA // IG. Mặt 0,25
 khác IG  BDG , SA  BDG nên SA // (BDG). 0,25
 Cách khác: G’O là đường trung bình của tam giác SAC nên 
 OG’//SA. Do OG '  BDG , SA  BDG nên SA//(BDG)
 u7 u2 15 5d 15
 Ta có 
 u4 u6 20 2u1 8d 20 0,25
 a 0,5
 d 3
 0,25
 u1 2
 n
13A S 2u n 1 d 
 n 2 1 
 n 2
 115 4 3 n 1 230 3n 7n 0,25
 2 
 b 0,5
 n 10(N)
 3n2 7n 230 0 23
 n (L)
 3 0,25
 Vậy n = 10
 Đk: x 3 , x N
 x! x! x(x 1)(x 2)
 C 3 5C1 5 5x 2x0,25
 x x 3!(x 3)! 1!(x 1)! 6
 x 3 3x 2 28x 0
14A 1,0
 x 0(l)
 x 0
 x 7 2x0,25
 2 
 x 3x 28 0
 x 4(l)
 Vậy x=7
 6 0,25
 a n() C14 3003 0,25
 Trong trường hợp này phải chọn cả 6 bạn nam, vậy có C 6 = 0,25
15A 8
 b 28 cách chọn. 0,5
 0,25