Bộ đề kiểm tra 1 tiết chương IV môn Đại số 10 - Năm học 2016-2017 - Trường THPT Nguyễn Văn Cừ (Có đáp án)

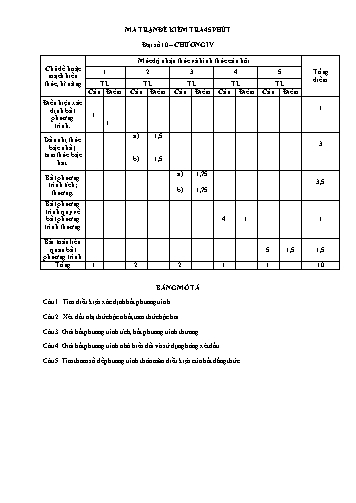
 MA TRẬN ĐỀ KIỂM TRA 45 PHÚT 
 Đại số 10 – CHƯƠNG IV
 Mức độ nhận thức và hình thức câu hỏi
Chủ đề hoặc 
 1 2 3 4 5 Tổng
 mạch kiến 
 điểm
thức, kĩ năng TL TL TL TL TL
 Câu Điểm Câu Điểm Câu Điểm Câu Điểm Câu Điểm
Điều kiện xác 
 định bất 1
 phương 1
 trình. 1
 a) 1,5
Dấu nhị thức 
 3
 bậc nhất, 
tam thức bậc 
 b) 1,5
 hai.
 a) 1,75
 Bất phương 
 3,5
 trình tích; 
 b) 1,75
 thương.
 Bất phương 
trình quy về 
 bất phương 4 1 1
trình thương
Bài toán liên 
 quan bất 5 1,5 1,5
phương trình
 Tổng 1 2 2 1 1 10
 BẢNG MÔ TẢ
Câu 1. Tìm điều kiện xác định bất phương trình. 
Câu 2. Xét dấu nhị thức bậc nhất, tam thức bậc hai.
Câu 3. Giải bất phương trình tích, bất phương trình thương. 
Câu 4. Giải bất phương trình nhờ biến đổi và sử dụng bảng xét dấu. 
Câu 5. Tìm tham số để phương trình thỏa mãn điều kiện của bất đẳng thức. Đáp án (Đại số 10, Đề 01)
 CÂU ĐÁP ÁN ĐIỂM
 Câu 1 x 0 x 0 0,5 điểm
 (1 Điều kiện: 
 điểm) x 1 0 x 1 0,5 điểm
 Vậy để bất phương trình đã cho có nghĩa thì x 0 và x 1 . 
 Câu 2 a) Nhị thức f x 2x 3 có hệ số a 2 0 và 2x 3 0 x 3 2 .
 (3 0,25
 Bảng xét dấu: 
 điểm)
 x 3 2 
 f x 0 
 Suy ra f x 0 , x 3 2; ; f x 0 , x ;3 2 .
 1,25
 b) Tam thức f x 3x2 x 2 có hệ số a 3 0 và
 2 x 2 3 0,25 
 3x x 2 0 .
 x 1
 Bảng xét dấu:
 x 2 3 1 
 f x + 0 0 +
 Suy ra f x 0 , x ; 2 3  1; ; f x 0 ,x 2 3;1 
 1,25
Câu 3 a) x 2 x2 2x 3 0 
(3,5 
điểm) Đặt f x x 2 x2 2x 3 .
 Nhị thức bậc nhất x 2 và tam thức bậc hai x2 2x 3 đều có hệ số 
 a 1 0 và lần lượt có các nghiệm x 2 và x 1 hoặc x 3 . 0.5
 Bảng xét dấu:
 x 1 2 3 
 x 2 | 0 + | +
 x2 2x 3 + 0 | 0 +
 f x 0 + 0 0 +
 Suy ra , .
 f x 0 x  1;2 3; 1.25
 3x2 7x 6
 b) 0 
 2x 1
 3x2 7x 6
 Đặt f x .
 2x 1
 Nhị thức bậc nhất 2x 1 và tam thức bậc hai 3x2 7x 6 đều có hệ số 
 a 0 và lần lượt có các nghiệm x 1 2 và x 3 hoặc x 2 3. 0.5
 Bảng xét dấu:
 x 3 1 2 2 3 
 3x2 7x 6 + 0 | 0 +
 2x 1 | 0 + | + 1,25 TRƯỜNG THPT NGUYỄN VĂN CỪ KIỂM TRA 1 TIẾT ĐẠI SỐ 10 – CHƯƠNG IV
 TỔ TOÁN - TIN Năm học: 2016 – 2017 ; Tiết PPCT: 45
 ĐỀ CHÍNH THỨC Thời gian làm bài: 45 phút (không kể thời gian giao đề)
 ĐỀ 02
 1
Câu 1. (1 điểm) Tìm x để bất phương trình x 0 có nghĩa.
 x 2
Câu 2. (3 điểm) Xét dấu a) f x 3x 3 ; b) f x x2 4x 5 . 
Câu 3. (3,5 điểm) Giải các bất phương trình sau: 
 2x2 x 6
a) x 1 x2 2x 3 0 b) 0 
 x 3
 x 2 x 1
Câu 4. (1 điểm) Giải bất phương trình: 1 . 
 x 1 x
Câu 5. (1,5 điểm) Tìm tham số m để: mx2 2 m 1 x 4m 1 0 có hai nghiệm dương thỏa 
 2 2
mãn x1 x2 0 . 
 ----------Hết--------
 Họ tên học sinh:..: Lớp. 1.25
Câu 4 x 2 x 1
 Giải: 1 1 
(1 x 1 x
điểm)
 x 2 x 1 x 2 x x x 1 x 1 x 1 
 1 1 0 0 
 x 1 x x2 x
 x2 x 1
 2 0 .
 x x 0,25
 x2 x 1
 Đặt f x 
 x2 x
 2 2
 Hai tam thức bậc hai x x 1 và x x lần lượt có hệ số a 0 và a 0 
 và lần lượt có các nghiệm x 1 5 2 hoặc x 1 5 2 và x 0 
 hoặc x 1. 
 Bảng xét dấu:
 x 1 1 5 2 0 1 5 2 
 x2 x 1 | 0 + | + 0 
 x2 x + 0 | 0 + | +
 f x || + 0 || + 0 
 0,75
 Suy ra f x 0 , x ; 1  1 5 2;0  1 5 2; .
Câu 5 mx2 2 m 1 x 4m 1 0
(1,5 
 Phương trình đã cho có hai nghiệm dương 
điểm)
 m 0
 m 0 
 ' 0 1 13 6 m 1 13 6
 c a 0 4m 1 m 0
 b a 0 
 2 m 1 m 0
 m 0
 1 13 6 m 1 13 6
 1 13 6 m 0 1 0.5
 m 0 hoac m 1 4
 m 0 hoac m 1
 2 2 2
 Hai nghiệm dương thỏa mãn x1 x2 0 x1 x2 2x1x2 0
 2
 2 m 1 4m 1 4m2 6m 4
 2. 0 2 0 
 m m m
 m 2
 2 .
 m 1 2 0.5
 Kết hợp 1 và 2 suy ra không tồn tại giá trị m thỏa mãn yêu cầu bài toán. 
 0,5
 -----------------Hết------------- TRƯỜNG THPT NGUYỄN VĂN CỪ KIỂM TRA 1 TIẾT – ĐS-GT 11 – CHƯƠNG IV
 TỔ TOÁN - TIN Năm học: 2016 – 2017; Tiết PPCT: 62
 ĐỀ CHÍNH THỨC Thời gian làm bài: 45 phút (không kể thời gian giao đề) 
 Đề 01
 2n 1 x2 3x 5
Câu 1. (3,5 điểm) Tính a) lim ; b) lim x3 2x2 x 3 ; c) lim ; 
 n 2 x x 3 x 3
 1 2x x2 5x 6
Câu 2. (4,5 điểm) Tính a) lim ; b) lim .
 x 2 x 2 x 3 x 3
 x3 8
 khi x 2
 c) Tìm m để hàm số f x x 2 liên tục tại điểm x 2.
 mx 1 khi x 2
Câu 3. (2 điểm) a) Chứng minh rằng phương trình: x3 8x2 4 0 có ít nhất hai nghiệm. 
 3 3x 2 4x2 x 2
 b) Tính lim . 
 x 1 x2 3x 2
 ----------Hết--------
 Họ tên học sinh: Lớp. 2
 3 3x 2 1 3 3x 2 3 3x 2 1
 3 3x 2 1 
I lim lim
 x 1 2 x 1 2
 x 3x 2 x2 3x 2 3 3x 2 3 3x 2 1 
 3x 2 1
 lim
 x 1 2
 x2 3x 2 3 3x 2 3 3x 2 1 
 3 x 1 
 lim
 x 1 2
 x 2 x 1 3 3x 2 3 3x 2 1 
 3
 lim 1
 x 1 2
 x 2 3 3x 2 3 3x 2 1 
 2 2
 1 4x2 x 2 1 4x x 2 1 4x x 2 
J lim 2 lim
 x 1 x 3x 2 x 1 x2 3x 2 1 4x2 x 2 
 1 4x2 x 2 4 x 1 x 3 4 
 lim lim
 x 1 x 2 x 1 1 4x2 x 2 x 1 x 2 x 1 1 4x2 x 2 
 4 x 3 4 7
 lim 
 x 1 x 2 1 4x2 x 2 2 
 0.75
 3 3x 2 4x2 x 2 5
 lim 2 I J 
Vậy x 1 x 3x 2 2 
 ------------Hết------------- Đáp án (ĐS-GT 11, Đề 02)
 CÂ ĐÁP ÁN ĐIỂ
 U M
Câu n 2 n 1 2 n 1 2 n lim 1 2 n 1
1 a) lim lim lim 1
 2n 1 n 2 1 n 2 1 n lim 2 1 n 2
 3 2 3 2 3 
 lim x x 2x 1 lim x 1 1 x 2 x 1 x 
 b) x x 1.25
 lim x3. lim 1 1 x 2 x2 1 x3 .1 
 x x 
 2 2
 x2 2x 5 lim x 2x 5 lim x lim 2x lim 5
 lim x 2 x 2 x 2 x 2
 x 2 x 3 lim x 3 lim x lim 3 1.25
 c) x 2 x 2 x 2
 2 2 2. 2 5
 1
 2 3
Câu 1 2x
 a) lim
2 
 x 1 x 1
 Ta có 0.5
 lim 1 2x 1 2. 1 1 0
 x 1 
 lim x 1 0; x 1 0, x 1
 0.5
 x 1 
 1 2x
 lim 
 0.5
 x 1 x 1 
 x2 3x 2 x 1 x 2 
 b) lim lim lim x 2 1 2 1 1
 x 1 x 1 x 1 x 1 x 1
 c) TXĐ: D ¡ , x 3 ¡ . 0.25
 Ta có: 
 2
 x3 27 x 3 x 3x 9 
 lim f x lim lim lim x2 3x 9 27 0.5
 x 3 x 3 x 3 x 3 x 3 x 3
 f 3 3a 2 . 0.25
 Để hàm số liên tục tại x 2 thì lim f x f 3 27 3a 2 m 25 3 .
 x 3 0.75
 Vậy a 25 3 là giá trị cần tìm. 0.25
Câu a) Xét f x 2x3 10x2 7 là hàm đa thức nên liên tục trên ¡ . Do đó nó liên tục 
3
 trên các đoạn  1;0 và 0;1. 1 0.25
 Mặt khác, f 1 1; f 0 7; f 1 5 . 
 Do đó f 1 . f 0 0; f 0 . f 1 0 2 
 Từ 1 và 2 suy ra 2x3 10x2 7 0 có ít nhất hai nghiệm, một nghiệm thuộc 
 1;0 , còn nghiệm kia thuộc 0;1 . 0.75
 3 3x 2 4x2 x 2 3 3x 2 1 1 4x2 x 2
 b) lim lim
 x 1 x2 3x 2 x 1 x2 3x 2
 3 3x 2 1 1 4x2 x 2 3 3x 2 1 1 4x2 x 2
 lim lim lim
 x 1 2 2 x 1 2 x 1 2
 x 3x 2 x 3x 2 x 3x 2 x 3x 2
 I J 0.25