Bộ đề kiểm tra học kì II môn Toán 11 - Trường THPT Krông Ana (Có đáp án)

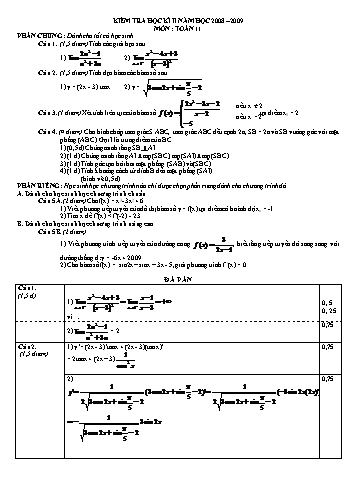
 KIỂM TRA HỌC KÌ II NĂM HỌC 2008 – 2009
 MÔN : TOÁN 11
PHẦN CHUNG : Dành cho tất cả học sinh
 Câu 1. (1,5 điểm) Tính các giới hạn sau
 2n 2 1 x 2 4x 3
 1) lim 2) lim .
 n 2 3n x 3 x 3 2
 Câu 2. (1,5 điểm) Tính đạo hàm các hàm số sau
 1) y = (2x - 3).tanx 2) y = 3cos 2x sin 2 .
 5
 2x 2 3x 2
 nếu x ≠ 2
 Câu 3. (1 điểm) Xét tính liên tục của hàm số f (x) x 2 tại điểm x0 = 2.
 nếu x =2
 5
 Câu 4. (4 điểm) Cho hình chóp tam giác S.ABC, tam giác ABC đều cạnh 2a, SB = 2a và SB vuông góc với mặt 
 phẳng (ABC). Gọi I là trung điểm của BC.
 1) (0,5đ) Chứng minh rằng SB  AI.
 2) (1 đ) Chứng minh rằng AI  mp(SBC), mp(SAI)  mp(SBC).
 3) (1 đ) Tính góc tạo bởi hai mặt phẳng (SAB) và (SBC).
 4) (1 đ) Tính khoảng cách từ đỉnh B đến mặt phẳng (SAI) .
 (hình vẽ 0,5đ) 
PHẦN RIÊNG : Học sinh học chương trình nào chỉ được chọn phần riêng dành cho chương trình đó
A. Dành cho học sinh học chương trình chuẩn
 Câu 5A. (2 điểm) Cho f(x) = x3- 3x2 + 6 .
 1) Viết phương tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ xo = -1.
 2) Tìm x để f’(x) < f’(-2) - 23.
B. Dành cho học sinh học chương trình nâng cao
 Câu 5B. (2 điểm) 
 3
 1) Viết phương trình tiếp tuyến của đường cong f (x) , biết rằng tiếp tuyến đó song song với 
 2x 1
 đường thẳng d: y = -6x + 2009.
 2) Cho hàm số f(x) = sin2x – sinx – 3x - 5, giải phương trình f ‘(x) = 0.
 Đ Á P ÁN
Câu 1. 
(1,5 đ) x 2 4x 3 x 1
 1) lim lim 0, 5
 x 3 2 x 3 
 x 3 x 3 0, 25
 vì 
 2n 2 1 0,75
 2) lim = 2
 n 2 3n
Câu 2. 1) y’= (2x - 3)’tanx + (2x - 3)(tanx)’ 0,75
 (1,5 điểm) 1
 = 2tanx + (2x – 3)
 cos 2 x
 2) 0,75
 1 1
 y' (3cos 2x sin 2)' ( 3sin 2x(2x)')
 5 
 2 3cos 2x sin 2 2 3cos 2x sin 2
 5 5
 1
 3sin 2x
 3cos 2x sin 2
 5 6
 Theo gt, =-6 => x0= 0 v x0= 1
 2x 1 2
 0 0,5
 * x0= 0, M(0; -3)
 d: y= -6x – 3
 x0= 0, M(0; -3)
 d: y= -6(x – 1) – 3
 (d: y= -6x + 3)
 2) sin2x – sinx – 3x – 5
 f’(x)= 0
 2cos2x – cosx -3 = 0
 2(2cos2x – 1) - cosx -3 = 0
 4cos2x – cosx -5 = 0
 cosx = -1 v cosx = +5/4(ko có x)
 x k2 ,k Z
Sở GD & ĐT ĐakLak KIỂM TRA HỌC KÌ II – NĂM HỌC 2009-2010
TRƯỜNG THPT KRÔNG ANA MÔN TOÁN 11
Phần chung (7 điểm)
Bài 1 (1,75 điểm) Tìm đạo hàm của mỗi hàm số sau
 3
 2x 5 2 3
a) y b) y x 3x 4
 x 1 
Bài 2 (0,75 điểm) Một chất điểm chuyển động với phương trình S t3 6t 5 (m) (t tính bằng giây (s)). Tính vận tốc 
của chất điểm đó tại thời điểm t 4(s) .
Bài 3 (1 điểm) Chứng minh rằng phương trình sau luôn có nghiệm với mọi giá trị của tham số m:
 1 m2 x5 3x 1 0 .
Bài 4 (3,5 điểm) Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng a 5 .
 a) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (SBD).
 b) Tính góc giữa hai mặt phẳng (SCD) và mặt phẳng (ABCD).
 c) Xác định và tính độ dài đoạn vuông góc chung của BD và SC.
 d) Tính khoảng cách từ điểm O đến mặt phẳng (SCD).
Phần riêng (3 điểm) Học sinh học theo chương trình nào chỉ được làm bài theo chương trình đó
A) Dành cho chương trình chuẩn
Bài 5A (2 điểm) Tính các giới hạn sau
 x 3 3 1 cos3x
a) lim 2 b) lim 2
 x 6 x 6 x 0 x
 1
Bài 6A (1 điểm) Cho các hàm số f (x) sin4 x cos4 x, g(x) cos 4x . 
 4
Chứng minh rằng f (x) g(x) ' 0
B) Dành cho chương trình nâng cao
 u1 1
Bài 5B) (2 điểm) Cho dãy un xác định bởi 
 un 1 2un 5,n 1
 a. CM vn là một cấp số nhân với vn un 5 .
 b. Tính limun .
Bài 6B) (1 điểm) Cho hàm số y x3 x2 x 1 có đồ thị là (C).
Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của nó với đường thẳng y 1 x .
 HẾT
 ĐÁP ÁN 
 Nội dung Điểm 
 Câu Ý Trong tam giác SOC kẻ đường cao OH  SC (1) 0,25
 Mà BD  (SAC) và OH  (SAC) OH  BD (2)
 Từ (1) và (2) suy ra OH là đường vuông góc chung của SC và BD.
 Vậy d(SC;BD) OH 0,25
 Trong tam giác vuông SOC có:
 1 1 1 1 1 2 2 8
 OH 2 SO2 OC2 SC2 OC2 OC2 3a2 a2 3a2
 a 6
 OH 
 4
 AB // CD
 CD // SAB  SA
 Ta có CD  SAB 0,25
 d)
 d CD, SA d CD, SAB d I, SAB 
 1,25
 Gọi M là trung điểm AB, từ I kẻ IN  SM , N SM IN  SAB 0,25
 d I, SAB IN 2OK ' , với OK '  SM tại K’
 Tam giác SOM vuông tại O và có OK’ là đường cao nên
 1 1 1 1 1 14 a 42
 2 2 2 2 2 2 K 'O 0,25
 K 'O OM OS a a 6 3a 14
 2 
 2 
 a 42
 Vậy d CD, SA .
 7
 (hoặc tính trực tiếp IN dựa vào hệ thức IN. SM = SO. IM)
 Đặt f (x) = mx3 + nx + p , ta thấy f(x) là hàm đa thức nên liên tục trên 0,25
 é 3ù
 ê0; ú.
 ëê 2ûú
 Mặt khác f(0) = p, 
 æ3ö 27 3
 f ç ÷= m + n + p
 èç2ø÷ 8 2
 3 11
 = (9m + 4n + 10 p)- p
 8 4
 0,25
 11
 Câu 3 (1 
 = - p 1,0
 điểm) 4
 æ3ö p2 0,25
 Þ f (0). f ç ÷= -
 èç2ø÷ 4
 Nếu p = 0 thì phương trình f(x) = 0 có ít nhất 1 nghiệm dương là 3/2.
 æ3ö p2 0,25
 Nếu p ¹ 0 thì f (0). f ç ÷= - < 0 nên phương trình f(x) = 0 có ít 
 èç2ø÷ 4
 æ ö
 ç 3÷
 nhất 1 nghiệm dương x0 Î ç0; ÷.
 èç 2ø÷
 Vậy phương trình f(x) = 0 luôn có ít nhất 1 nghiệm dương với điều kiện đã 
 cho.
 1 2 3 0,5+0,25
 f '(x) . 2x 'sin 2x sin 2x f ' sin 
 2 3 3 2
 0,25x2
 Câu 4a. 3
 f ''(x) 2 cos2x f '' 2 cos 2. 3 1,5
(1,5 điểm) 12 6 2 0,25
 3
 Vậy 2 f ' f '' 2 3 0
 3 12 2 SỞ GIÁO DỤC & ĐÀO TẠO ĐĂKLĂK KIỂM TRA HỌC KÌ 2, NĂM HỌC 2011-2012
ĐỀ CHÍNH THỨC
I. Phần chung (7 điểm)
Câu 1. (1,5 điểm) Tính các giới hạn sau
 3
 a) lim b) lim (3x x3 ) c) lim ( x2 x 3 x) 
 x 1 x 1 x x 
Câu 2. (1 điểm) Tìm đạo hàm của các hàm số sau
 a) y 2sin x 6cos x b) y x2 x cot 2x 1
 x2 2x 3
 ; (x 3)
 x 3
Câu 3. (1 điểm) Cho hàm số f (x) (m tham số). 
 2m
 x 
 m2 12
Tìm m để hàm số liên tục tại x 3 .
 a 6
Câu 4. (3,5 điểm) Cho hình chóp S.ABCD, có đáy ABCD là hình vuông tâm O cạnh a , cạnh bên SA , 
 2
SA  ABCD .
 a) Chứng minh đường thẳng CD vuông góc mặt phẳng (SAD) và mặt phẳng (SAB) vuông góc với mặt phẳng 
(SAD).
 b) Xác định và tính góc giữa hai mặt phẳng (SBD) và (ABCD).
 c) Tính khoảng cách từ A đến mặt phẳng (SBC); Xác định và tính khoảng cách giữa hai đường thẳng chéo nhau 
BD và SC.
II. Phần riêng (3 điểm) 
Học sinh học theo chương trình nào chỉ được làm bài theo phần riêng chương trình đó.
A) Theo chương trình chuẩn.
Câu 5a. ( 2 điểm) Cho hàm số y f (x) x4 x2 3 có đồ thị là C . 
 1) Tính vi phân dy của hàm số đã cho. 
 2) Viết phương trình tiếp tuyến của C tại điểm có tung độ bằng 3.
 x 3
Câu 6a. (1 điểm) Cho hàm số: y . Tính y '; y ''. Từ đó chứng minh: 2(y ')2 (y 1)y '' .
 x 4
B) Theo chương trình nâng cao
Câu 5b. (2 điểm) Cho hàm số y f (x) x4 x2 3 có đồ thị là C .
 1) Tính vi phân dy của hàm số đã cho. Tìm x thoả f ''(x) 10 .
 2) Viết phương trình tiếp tuyến của C biết tiếp tuyến vuông góc với đường thẳng d: x 2y 3 0 .
 u1 2;u2 3
Câu 6b. (1 điểm) Cho dãy số un được xác định như sau: ,n 2 , 
 u 3u 2u
 n 1 n n 1
đặt vn un 1 un ,n 1 .Chứng minh vn là một cấp số nhân. Tìm số hạng tổng quát của un .
 HẾT.
 KIỂM TRA HỌC KÌ 2, NĂM HỌC 2012-2013
I. Phần chung (7 điểm)
 Câu I. ( 1,5 điểm) Tìm các giới hạn sau:
 2x 1
 1) lim ; 2) lim ( x3 x2 3x 1)
 x 5 x 5 x 
 Câu II. ( 1,0 điểm) Tính đạo hàm của hàm số sau:
 x3
 1) y sin x ; 2) y x2 x 1
 3
 Câu III. ( 3,5 điểm) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2 a , cạnh bên bằng a 5 . Gọi I là trung 
điểm của AB, O là giao điểm của AC và BD.
 1) Chứng minh rằng: AB  SIO . Từ đó chứng minh: SIO  SAB .