Đề tham khảo thi tốt nghiệp THPT năm 2021 môn Toán - Trường THPT Trần Quốc Toản (Có đáp án)

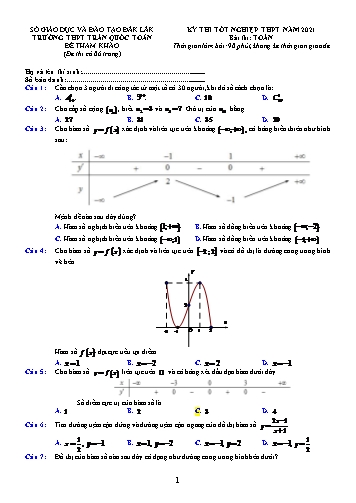
 SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐẮK LẮK KỲ THI TỐT NGHIỆP THPT NĂM 2021 
 TRƯỜNG THPT TRẦN QUỐC TOẢN Bài thi: TOÁN
 ĐỀ THAM KHẢO Thời gian làm bài: 90 phút, không kể thời gian giao đề
 (Đề thi có 06 trang)
Họ và tên thí sinh:..................................................................... 
Số báo danh: .............................................................................
Câu 1: Cần chọn 3 người đi công tác từ một tổ có 30 người, khi đó số cách chọn là:
 3 30 3
 A. A30 . B. 3 . C. 10. D. C30 .
Câu 2: Cho cấp số cộng un , biết u2 3 và u4 7. Giá trị của u15 bằng
 A. 27 . B. 31. C. 35 . D. 29 .
Câu 3: Cho hàm số y f x xác định và liên tục trên khoảng ; , có bảng biến thiên như hình 
 sau:
 Mệnh đề nào sau đây đúng?
 A. Hàm số nghịch biến trên khoảng 1; . B. Hàm số đồng biến trên khoảng ; 2 .
 C. Hàm số nghịch biến trên khoảng ;1 . D. Hàm số đồng biến trên khoảng 1; .
Câu 4: Cho hàm số y f x xác định và liên tục trên  2;2 và có đồ thị là đường cong trong hình 
 vẽ bên.
 y
 4
 2
 x
 -2 -1 O 1 2
 Hàm số f x đạt cực tiểu tại điểm
 A. x 1. B. x 2. C. x 2 . D. x 1.
Câu 5: Cho hàm số y f x liên tục trên ¡ và có bảng xét dấu đạo hàm dưới đây
 .
 Số điểm cực trị của hàm số là
 A. 1. B. 2 . C. 3. D. 4 .
 2x 1
Câu 6: Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y .
 x 1
 1 1
 A. x , y 1. B. x 1, y 2 . C. x 1, y 2 . D. x 1, y .
 2 2
Câu 7: Đồ thị của hàm số nào sau đây có dạng như đường cong trong hình bên dưới?
 1 A. 2 11i . B. 3 9i . C. 3 9i . D. 2 11i .
Câu 20: Số phức nào có biểu diễn hình học là điểm M trong hình vẽ dưới đây?
 A. z 2 i . B. z 1 2i . C. z 2 i . D. z 1 2i .
Câu 21: Một khối chóp có đáy là hình vuông cạnh bằng 2 và chiều cao bằng 6. Thể tích của khối chóp 
 đó bằng
 A. 24 . B. 8 . C. 4 . D. 12.
Câu 22: Một khối lập phương có thể tích bằng 64cm2 . Độ dài mỗi cạnh của khối lập phương đó bằng
 A. 4cm . B. 8cm . C. 2cm . D. 16cm .
Câu 23: Một hình nón có bán kính đáy r 4 và độ dài đường sinh l 5 . Diện tích xung quanh của hình 
 nón đó bằng
 A. 10 . B. 60 . C. 20 . D. 40 .
Câu 24: Công thức tính thể tích V của khối trụ có bán kính đáy r và chiều cao h là
 1 1
 A. V rh . B. V r 2h . C. V r 2h . D. V rh .
 3 3 
Câu 25: Trong không gian với hệ trục tọa độ Oxyz , cho a 1;2;0 , b 2;1;0 , c 3;1;1 . Tìm 
 tọa độ của vectơ u a 3b 2c .
 A. 10; 2;13 . B. 2;2; 7 . C. 2; 2;7 . D. 11;3; 2 .
Câu 26: Trong không gian Oxyz , cho mặt cầu S : x2 y2 z2 2y 4z 2 0 . Bán kính của mặt cầu 
 đã cho bằng
 A. 1. B. 7 . C. 2 2 . D. 7 .
Câu 27: Trong không gian Oxyz , cho 2 điểm A 1;0;1 , B 2;1;0 . Viết phương trình mặt phẳng P 
 đi qua A và vuông góc với AB .
 A. P :3x y z 4 0 . B. P :3x y z 4 0 .
 C. P :3x y z 0 . D. P : 2x y z 1 0.
 x 2 y 1 z 7
Câu 28: Trong không gian Oxyz , cho đường thẳng d : . Vectơ nào dưới đây không 
 1 3 5
 phải là một vectơ chỉ phương của d ?
     
 A. u4 1;3;5 . B. u3 1;3; 5 . C. u1 1; 3;5 . D. u2 2;6; 10 .
Câu 29: Trong một lớp học gồm 15 học sinh nam và 10 học sinh nữ. Giáo viên gọi ngẫu nhiên 4 học 
 sinh lên giải bài tập. Tính xác suất để 4 học sinh được gọi đó có cả nam và nữ?
 219 219 442 443
 A. . B. . C. . D. .
 323 323 506 506
Câu 30: Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó ?
 x - 2 x - 2 - x + 2 x + 2
 A. y = . B. y = . C. y = . D. y = .
 - x + 2 x + 2 x + 2 - x + 2
Câu 31: Gọi m là giá trị nhỏ nhất và M là giá trị lớn nhất của hàm số f (x)= 2x3 + 3x2 - 1 trên đoạn 
 é 1ù
 ê- 2;- ú. Khi đó giá trị của M - m bằng
 ëê 2ûú
 A. - 5 . B. 1. C. 4. D. 5.
 3 Số điểm cực trị của hàm số y f ( x ) là
 A. 0. B. 1. C. 3. D. 2.
Câu 40: Gọi S là tổng tất cả các giá trị nguyên của m để bất phương trình 
 ln 7x2 7 ln mx2 4x m nghiệm đúng với mọi x thuộc ¡ . Tính S .
 A. .S 14 B. . S 0 C. . SD. .12 S 35
 3
 e f lnx 2
Câu 41: Cho hàm số f x liên tục trên ¡ . Biết dx 7 , f cos x .sin xdx 3 . Tính 
 1 x 0
 3
 f x 2x dx .
 1
 A. .1 2 B. . 15 C. . 10 D. . 10
Câu 42: Cho số phức z a bi a,b ¡ thỏa mãn điều kiện z2 4 2 z . Đặt P 8 b2 a2 12. 
 Mệnh đề nào dưới đây đúng?
 2 2 2 2
 A. .P z 2B. 4. C. . P D. z . 2 P z 4 P z 2 2 
Câu 43: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Hình chiếu của S trên mặt phẳng 
 3a
 ABCD trùng với trung điểm của cạnh AB . Cạnh bên SD . Tính thể tích khối chóp 
 2
 S.ABCD theo a .
 1 3 5 2
 A. . a3 B. . a3 C. . D.a 3. a3
 3 3 3 3
Câu 44: Một viên gạch hoa hình vuông cạnh 40 cm được thiết kế như hình bên dưới. Diện tích mỗi 
 cánh hoa bằng
 y 1
 y = x2
 20
 y = 20x
 20
 x
 20 20
 20
 800 400
 A. . cm2 B. . cm2 C. . 250 cD.m2 . 800 cm2
 3 3
 5 BẢNG ĐÁP ÁN
 1.D 2.D 3.B 4.D 5.C 6.C 7.A 8.A 9.C 10.B
 11.D 12.D 13.C 14.B 15.B 16.A 17.B 18.B 19.D 20.A
 21.B 22.A 23.C 24.C 25.D 26.B 27.A 28.A 29.D 30.C
 31.D 32.B 33.B 34.D 35.B 36.D 37.D 38.D 39.D 40.C
 41.A 42.D 43.A 44.B 45.C 46.B 47.B 48.A 49.C 50.A
 HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cần chọn 3 người đi công tác từ một tổ có 30 người, khi đó số cách chọn là:
 3 30 3
 A. A30 . B. 3 . C. 10. D. C30 .
 Lời giải
 Chọn 3 người đi công tác từ một tổ có 30 người là một tổ hợp chập 3 của 30 phần tử, nên có 
 3
 C30 cách.
Câu 2: Cho cấp số cộng un , biết u2 3 và u4 7. Giá trị của u15 bằng
 A. 27 . B. 31. C. 35 . D. 29 .
 Lời giải
 u1 d 3 u1 1
 Từ giả thiết u2 3 và u4 7 suy ra ta có hệ phương trình: .
 u1 3d 7 d 2
 Vậy u15 u1 14d 29 .
Câu 3: Cho hàm số y f x xác định và liên tục trên khoảng ; , có bảng biến thiên như hình 
 sau:
 Mệnh đề nào sau đây đúng?
 A. Hàm số nghịch biến trên khoảng 1; . B. Hàm số đồng biến trên khoảng ; 2 .
 C. Hàm số nghịch biến trên khoảng ;1 . D. Hàm số đồng biến trên khoảng 1; .
 Lời giải
 Từ bảng biến thiên ta thấy hàm số đồng biến trên khoảng ; 1 , suy ra hàm số cũng đồng 
 biến trên khoảng ; 2 .
Câu 4: Cho hàm số y f x xác định và liên tục trên  2;2 và có đồ thị là đường cong trong hình 
 vẽ bên.
 7 A. y x3 x 1. B. y x3 x 1. C. y x3 x 1. D. y x3 x 1.
 Lời giải
 Nhìn vào hình vẽ ta thấy đồ thị cắt trục tung tại điểm có tung độ dương nên loại các đáp án 
 y x3 x 1 và y x3 x 1.
 Ta thấy đồ thị hàm số không có cực trị nên chọn đáp án y x3 x 1 vì hàm số này có 
 y ' 3x2 1 0,x .
Câu 8: Số giao điểm của đồ thị của hàm số y x4 4x2 3 với trục hoành là
 A. 2 . B. 0 . C. 4 . D. 1.
 Lời giải
 x2 1
 Ta có y x4 4x2 3 0 x 1.
 2
 x 3(PTVN)
 Suy ra đồ thị hàm số có 2 giao điểm với trục hoành.
 4
Câu 9: Với a là số thực dương tùy ý, log bằng
 2 a
 1
 A. log a . B. 2log a . C. 2 log a . D. log a 1.
 2 2 2 2 2
 Lời giải
 4
 Ta có: log log 4 log a 2 log a .
 2 a 2 2 2
Câu 10: Đạo hàm của hàm số y 3x là
 1 3x
 A. log a . B. y ' 3x ln 3. C. y ' . D. ln 3.
 2 2 ln 3
 Lời giải
 Dùng công thức a x ' a x ln a 3x ' 3x ln 3 .
Câu 11: Với a là số thực dương tùy ý, 3 a2 bằng
 5 1 2
 A. a3 . B. a 3 . C. a 3 . D. a 3 .
 Lời giải
 m 2
 Với a 0 dùng công thức n am a n 3 a2 a 3 .
Câu 12: Nghiệm của phương trình 34x 6 9 là
 A. x 3. B. x 3. C. x 0 . D. x 2 .
 Lời giải
 9