Đề thi chọn học sinh giỏi cấp trường môn Toán 11 - Năm học 2018-2019 - Hoàng Minh Tài (Có đáp án)

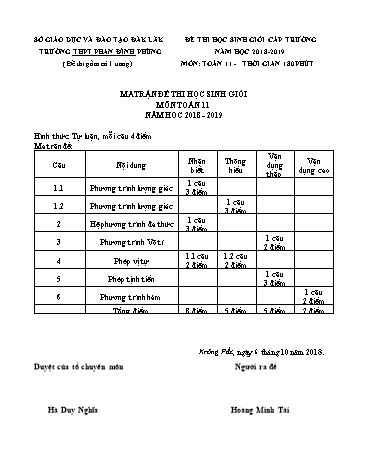
 SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐĂK LẮK ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG
 TRƯỜNG THPT PHAN ĐÌNH PHÙNG NĂM HỌC 2018- 2019
 ( Đề thi gồm có 1 trang) MÔN: TOÁN 11 - THỜI GIAN 180 PHÚT 
 MA TRẬN ĐỀ THI HỌC SINH GIỎI 
 MÔN TOÁN 11
 NĂM HOC 2018 - 2019
Hình thức: Tự luận, mỗi câu 4 điểm
Ma trận đề:
 Vận 
 Nhận Thông Vận 
 Câu Nội dung dụng 
 biết hiểu dụng cao
 thấp
 1 câu
 1.1 Phương trình lượng giác
 3 điểm
 1 câu
 1.2 Phương trình lượng giác
 3 điểm
 1 câu
 2 Hệ phương trình đa thức
 3 điểm
 1 câu
 3 Phương trình Vô tỉ 
 2 điểm
 1.1 câu 1.2 câu
 4 Phép vị tự
 2 điểm 2 điểm
 1 câu
 5 Phép tịnh tiến
 3 điểm
 1 câu
 6 Phương trình hàm
 2 điểm
 Tổng điểm 8 điểm 5 điểm 5 điểm 2 điểm
 Krông Pắc, ngày 6 tháng 10 năm 2018.
Duyệt của tổ chuyên môn Người ra đề
 Hà Duy Nghĩa Hoàng Minh Tài Krông Pắc, ngày 6 tháng 10 năm 2018.
Duyệt của tổ chuyên môn Người ra đề
 Hà Duy Nghĩa Hoàng Minh Tài 3 Điều kiện của phương trình: 12 x 4 1.0
 u x 3 u2 x2 6x 9
 Đặt u2 v2 57 2x
 2 2 2
 v x 8x 48 v 0 v x 8x 48
 Suy ra: Phương trình trở thành: 2uv u2 v2 1 u v 2 1
 v u 1 1.0
 v u 1
 + Với v u 1 và v 0 suy ra phương trình:
 x 2 0 x 2 0.5
 x 3 31
 2 2
 x 8x 48 x 2 x 6x 16 0
 + Với v u 1 và v 0 suy ra phương trình:
 x 4 0 x 4
 x 4 4 2 0.5
 2 2
 x 8x 48 x 4 x 8x 16 0
 Vậy phương trình có tập nghiệm S = 3 31; 4 4 2
3 Gọi A’, B’, C’ lần lượt là trung điểm của cạnh BC, CA, AB. 
 Ta có: 1.0x2
 V 1 : A A',B B',C C ' V 1 VABC VA'B'C '
 G; G; 
 2 2 
 Laị có: H là trực tâm của tam giác ABC, O là trực tâm của tam giác A’B’C’ 1.0
  1    
 Suy ra: V 1 H O GO GH GH 2GO
 G; 2
 2 1.0
4 Với H là trực tâm của tam giác BEK, ta có: 
 + EH  BK và AD  BK suy ra: EH / /KD (1) 0.5
 + KH  BE và DC  BE suy ra: KH / /CD (2)   
 0.5
 Từ (1) và (2) suy ra tứ giác KHED là hình bình hành nên DE KH và
 HE KD .  
 Khi đó phép tịnh tiến theo vec tơ KD biết: K D, H E, B B'.
   
 Suy ra T BH B'E và BH  KE nên B'E  KE 0.5
 KD 
 BH 2 B'E 2 B'K 2 KE 2 B'K BD b 
 = b2 a2
 2 2 0.5
 BH b a