Đề thi thử tốt nghiệp THPT năm 2021 môn Toán - Trường THPT Lăk (Có đáp án)

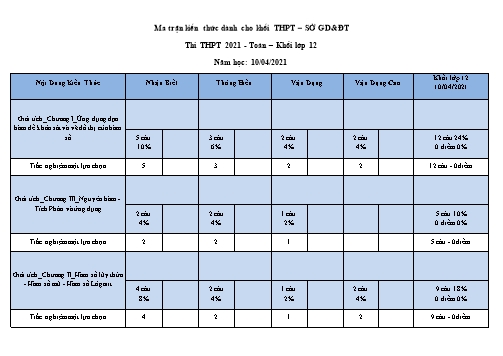
 Ma trận kiến thức dành cho khối THPT – SỞ GD&ĐT 
 Thi THPT 2021 - Toán – Khối lớp 12
 Năm học: 10/04/2021
 Khối lớp 12
 Nội Dung Kiến Thức Nhận Biết Thông Hiểu Vận Dụng Vận Dụng Cao
 10/04/2021
 Giải tích_Chương I_Ứng dụng đạo 
hàm để khảo sát và vẽ đồ thị của hàm 
 số 5 câu 3 câu 2 câu 2 câu 12 câu 24%
 10% 6% 4% 4% 0 điểm 0%
 Trắc nghiệm một lựa chọn 5 3 2 2 12 câu - 0điểm
 Giải tích_Chương III_Nguyên hàm - 
 Tích Phân và ứng dụng
 2 câu 2 câu 1 câu 5 câu 10%
 4% 4% 2% 0 điểm 0%
 Trắc nghiệm một lựa chọn 2 2 1 5 câu - 0điểm
Giải tích_Chương II_Hàm số lũy thừa 
 - Hàm số mũ - Hàm số Lôgarit
 4 câu 2 câu 1 câu 2 câu 9 câu 18%
 8% 4% 2% 4% 0 điểm 0%
 Trắc nghiệm một lựa chọn 4 2 1 2 9 câu - 0điểm Đại số tổ hợp - Xác suất
 1 câu 1 câu 2 câu 4%
 2% 2% 0 điểm 0%
 Trắc nghiệm một lựa chọn 1 1 2 câu - 0điểm
Dãy số - Cấp số cộng - Cấp số nhân
 1 câu 1 câu 2%
 2% 0 điểm 0%
 Trắc nghiệm một lựa chọn 1 1 câu - 0điểm
 Quan hệ vuông góc, khoảng cách
 2 câu 2 câu 4%
 4% 0 điểm 0%
 Trắc nghiệm một lựa chọn 2 2 câu - 0điểm
 25 câu - 50% 15 câu - 30% 5 câu - 10% 5 câu - 10% 50 câu - 100%
 0 điểm - 0% 0 điểm - 0% 0 điểm - 0% 0 điểm - 0% 10 điểm - 100% Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 A. ;1 . B. 1;1 . C. 0;1 . D. 1; .
Câu 11. Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 2a. Thể tích của khối 
lăng trụ đã cho bằng
 2 4
 A. a3 .B. a3 .C. 2a3 .D. 4a3 .
 3 3
Câu 12. Thể tích của khối trụ đường cao h và bán kính đáy r bằng
 1
 A. 2 r2h . B. rh2 . C. r2h . D. r2h .
 3
Câu 13. Cho hàm số f x có bảng biến thiên như sau:
 Điểm cực tiểu của hàm số đã cho là
 A. x 1. B. y 4. C. y 0. D. x 1.
 2
Câu 14. Tập nghiệm của phương trình log2 x 1 3 là
 A. 3;3 .B. 3. C. 3 .D. 10; 10.
 2x 1
Câu 15. Cho hàm số y có đồ thị C . Khẳng định nào đúng?
 x 1
 A.Đường tiệm cận ngang của C là đường thẳng y 2 .
 B. Đường tiệm cận đứng của C là đường thẳng x 1 .
 C. Đường tiệm cận ngang của C là đường thẳng x 1 .
 D. Đường tiệm cận đứng của C là đường thẳng y 2 .
Câu 16. Họ tất cả các nguyên hàm của hàm số f x 2x 6 là
 A. x2 6x C .B. 2x2 C .C. 2x2 6x C .D. x2 C .
Câu 17. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên dưới?
 y
 O
 x 2
Câu 29. Kí hiệu z1, z2 là hai nghiệm phức của phương trình z 4z 5 0 . Tính giá trị biểu thức 
 T z1 z2 .
 A.T 2 5 . B. T 5 . C. T 4 . D. T 8.
Câu 30. Tìm giá trị nhỏ nhất m của hàm số y x3 3x2 9x 5 trên đoạn  2;2.
 A. m 17 .B. m 6 .C. m 3 .D. m 22 .
Câu 31. Tìm tất cả các giá trị thực của tham số m để hàm số y log x2 2mx 4 có tập xác địnhlà 
 ¡ . 
 m 2
 A. . B. m 2. C. m 2. D. 2 m 2.
 m 2
Câu 32. Trong không gian với hệ tọa độ Oxyz, phương trình tham số của đường thẳng đi qua hai 
điểm P 1;2;3 ,Q 5;4;4 là
 x 1 4t x 5 4t x 1 t x 4 1t
 A. y 2 2t .B. y 4 2t . C. y 2 2t .D. y 2 2t .
 z 3 t z 4 t z 1 3t z 1 3t
Câu 33. Cho hình chóp S.ABCD có SA ^ (ABCD) và ABCD là hình vuông cạnh 2a, khoảng cách 
 2a 3
 từ C đến (SBD) là . Tính khoảng cách từ A đến (SCD).
 3
 A. a 3 .B. 2a . C. a 2 .D. 3a .
 2
Câu 34. Tính tích phân I cos4 xsin x dx bằng cách đặt t cos x , mệnh đề nào dưới đây đúng?
 0
 1 1 2 2
 A. I t 4dt .B. I t 4dt .C. I t 4dt .D. I t 4dt .
 0 0 0 0
Câu 35. Cho hàm số y f x liên tục trên ¡ . Gọi S là diện tích hình phẳng giới hạn bởi các 
đường y f x , y 0, x 1 và x 5 (như hình vẽ). Mệnh đề nào sau đây đúng?
 1 5 1 5
 A. S f x dx f x dx B. S f x dx f x dx
 1 1 1 1
 1 5 1 5
 C. S f x dx f x dx D. S f x dx f x dx
 1 1 1 1 A. a3 .B. 3 a3 .C. 4 a3 .D. 5 a3 .
 4
Câu 45. Cho hàm số f x . Biết f 0 4 và f x 2cos2 x 1,x ¡ , khi đó f x dx bằng
 0
 2 4 2 14 2 16 4 2 16 16
 A. . B. . C. . D. .
 16 16 16 16
Câu 46. Hàm số y f x có bảng biến thiên như sau
 x 1 3 
 f x 0 0 
 5 
 f x 
 1 2
 2
 Số nghiệm thực của phương trình x 1 f x 2 f x 3 0 là
 A. 0 . B. 3 . C. 6 . D. 9 .
 3 2
Câu 47. Cho m loga ab với a 1, b 1 và P loga b 16logb a . Tìm m sao cho P đạt giá trị 
 nhỏ nhất.
 1
 A. m .B. m 4 . C. m 1. D. m 2 .
 2
Câu 48. Cho hàm số f x x4 4x3 4x2 a . Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ 
 nhất của hàm số đã cho trên đoạn 0;2 . Có bao nhiêu số nguyên a thuộc đoạn  3;3 sao 
 cho M 2m ?
 A.3.B. 7 .C. 6 .D. 5.
Câu 49. Cho hình hộp ABCD.A B C D thể tích là V. Tính thể tích của tứ diện ACB D theo V.
 V V V V
 A. . B. . C. . D. .
 6 4 5 3
 3
Câu 50. Phương trình 2x 2 m 3x x3 6x2 9x m 2x 2 2x 1 1 có 3 nghiệm phân biệt khi và chỉ khi 
 m (a;b) đặt T b2 a2 thì:
 A. T 36 .B. T 48 .C. T 64 . D.T 72 .
 -----------HẾT----------