Sáng kiến kinh nghiệm Rèn luyện kỹ năng đọc đồ thị hàm số y= f'(x)

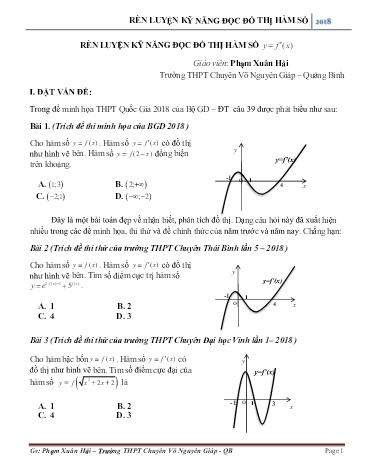
 RÈN LUYỆN KỸ NĂNG ĐỌC ĐỒ THỊ HÀM SỐ 2018 
 RÈN LUYỆN KỸ NĂNG ĐỌC ĐỒ THỊ HÀM SỐ y f () x 
 Giáo viên: Phạm Xuân Hải 
 Trường THPT Chuyên Võ Nguyên Giáp – Quảng Bình 
I. ĐẶT VẤN ĐỀ: 
Trong đề minh họa THPT Quốc Gia 2018 của Bộ GD – ĐT câu 39 được phát biểu như sau: 
Bài 1. (Trích đề thi minh họa của BGD 2018 ) 
Cho hàm số y f() x . Hàm số y f () x có đồ thị 
 y 
như hình vẽ bên. Hàm số y f(2 x ) đồng biến 
 y=f’(x) 
trên khoảng. 
 -1 
 O 1 
 A. 1;3 B. 2; 4 x 
 C. 2;1 D. ;2 
 Đây là một bài toán đẹp về nhận biết, phân tích đồ thị. Dạng câu hỏi này đã xuất hiện 
nhiều trong các đề minh họa, thi thử và đề chính thức của năm trước và năm nay. Chẳng hạn: 
Bài 2 (Trích đề thi thử của trường THPT Chuyên Thái Bình lần 5 – 2018 ) 
Cho hàm số . Hàm số có đồ thị 
 y 
như hình vẽ bên. Tìm số điểm cực trị hàm số 
 y=f’(x) 
ye 2f ( x ) 15 f ( x ) . 
 -1 1 
 A. 1 B. 2 O 4 x 
 C. 4 D. 3 
Bài 3 (Trích đề thi thử của trường THPT Chuyên Đại học Vinh lần 1– 2018 ) 
Cho hàm bậc bốn . Hàm số có y 
đồ thị như hình vẽ bên. Tìm số điểm cực đại của y=f’(x) 
hàm số y f x2 22 x là 
 -1 O 1 3 
 A. 1 B. 2 x 
 C. 4 D. 3 
Gv: Phạm Xuân Hải – Trường THPT Chuyên Võ Nguyên Giáp - QB Page 1 
 RÈN LUYỆN KỸ NĂNG ĐỌC ĐỒ THỊ HÀM SỐ 2018 
 Định lý 4. Trong mặt phẳng tọa độ Oxy, cho đồ thị (G) của hàm số y f() x ; p 
 và q là hai số dương tùy ý. Khi đó: 
 a. Tịnh tiến (G) lên trên q đơn vị thì được đồ thị của hàm số y f() x q 
 b. Tịnh tiến (G) xuống dưới q đơn vị thì được đồ thị của hàm số y f() x q 
 c. Tịnh tiến (G) sang trái p đơn vị thì được đồ thị của hàm số y f() x p 
 d. Tịnh tiến (G) sang phải p đơn vị thì được đồ thị của hàm số y f() x p 
 Định lý 5. 
 a. Nếu hàm số h h() x có đạo hàm tại điểm x0 và hàm số y g() h có đạo hàm 
 tại điểm h00 h() x thì hàm số hợp f()() x g h x  có đạo hàm tại điểm x0 và 
 f ( x0 ) g ( h 0 ). h ( x 0 ) 
 b. Nếu giả thiết trong phần a thỏa mãn đối với mọi điểm x thuộc J thì hàm số 
 hợp y f() x có đạo hàm trên J và f()().() x g h x h x . 
 Ghi chú: Công thức thứ hai trong định lý này còn được viết gọn là: f ghx . h . 
 b. Tịnh tiến (G) xuống dưới q đơn vị thì được đồ thị của hàm số 
 c. Tịnh tiến (G) sang trái p đơn vị thì được đồ thị của hàm số 
 d. Tịnh tiến (G) sang phải p đơn vị thì được đồ thị của hàm số 
Gv: Phạm Xuân Hải – Trường THPT Chuyên Võ Nguyên Giáp - QB Page 3 
 RÈN LUYỆN KỸ NĂNG ĐỌC ĐỒ THỊ HÀM SỐ 2018 
Hướng dẫn 
1.1) Dựa vào đồ thị ta lập được bảng biến thiên của hàm số đã cho như sau: 
 x -1 1 2 
 f’(x) - 0 + 0 - 0 + 
 f(1) 
 f(x) 
 f(-1) f(2) 
Dựa vào bảng biến thiên ta có các kết luận: 
Từ đồ thị hàm số y f () x hình 1, 
1.2) Xác định các khoảng đơn điệu 
 - Hàm số nghịch biến trên các khoảng ; 1 , 1;2 
 - Hàm số đồng biến trên các khoảng 1;1 , 2; 
1.3) Xác định cực trị của hàm số 
 - Hàm số đạt cực đại tại hai điểm xx 1; 2 , đạt cực tiểu tại x 1. 
1.4) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y f() x trên đoạn  1;4 
 Ta bảng biến thiên xác định được max y max f(1); f (4) và miny min f ( 1); f (2) 
  1;4  1;4
Để xác định được giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 
ta so sánh ff(1); (4)và ff( 1); (2) bằng cách: 
Đặt SSS1;; 2 3 lần lượt là diện tích hình phẳng được giới hạn bởi đồ thị hàm số , trục 
Ox trên các đoạn  1;1 , 1;2 , 2;4, từ hình 1 ta so sánh được SSSS1 2; 3 2 . 
 12
 S S f ( x ) dx f ( x ) dx f ( x )12 f ( x ) f (1) f ( 1) f (2) f (1)
+) 1 2 1 1 
 11
Suy ra : f( 1) f (2) f ( 1) f (2) . Nên minyf ( 1) 
  1;4
 42
 S S f ( x ) dx f ( x ) dx f ( x )42 f ( x ) f (4) f (2) f (2) f (1)
+) 3 2 2 1 
 21
Gv: Phạm Xuân Hải – Trường THPT Chuyên Võ Nguyên Giáp - QB Page 5 
 RÈN LUYỆN KỸ NĂNG ĐỌC ĐỒ THỊ HÀM SỐ 2018 
Cách 2: Sử` dụng định lý 4 ta có được đồ thị của hàm số fx ( 1) bằng cách tịnh tiến đồ thị 
(C) sang phải 1 đơn vị . Ta có đồ thị: y 
 2 
 (C’ ) y=f’(x-1) 
 -1 O 1 2 
 3 x 
 y f () x
 hình 2 
Nên số cực trị của hàm số y g( x ) f ( x 1) bằng số cực trị của hàm số y f() x . 
 Kết luận: Hàm số y g() x có 3 cực trị. 
1.8 Từ đồ thị hàm số ở hình 1,xác định số cực trị của hàm số h( x ) f ( x ) 2 x ? 
Cách 1. Lập bảng biến thiên của hàm số 
Cách 2. Sử dụng định lý 4. 
Ta có h ( x ) f ( x ) 2 . Nên ta có được đồ thị của hàm số h ( x ) f ( x ) 2 bằng cách tịnh tiến 
đồ thị (C) lên trên 2 đơn vị . Dựa vào đồ thị, ta kết luận hàm số hx() có 1 cực trị. 
 y 
 y=f’(x)+2 
 2 
 1 (C ) y=f’(x) 
 -1 1 2 
 O x 
 hình 1 
Gv: Phạm Xuân Hải – Trường THPT Chuyên Võ Nguyên Giáp - QB Page 7 
 RÈN LUYỆN KỸ NĂNG ĐỌC ĐỒ THỊ HÀM SỐ 2018 
Đặt g( x ) f x2 2 x 2 , ta có: 
 a x 13 x2 2 x 7
 2 2x 1 2 
g ( x ) x 2 x 2 . f x 2 x 2 . f x 2 x 2 
 2 
 xx 22 x22 2 x 2 x 2 x 2 3 
Lập bẳng biến thiên gx() ta có 
 x - 1 
 g’(x) - 0 + 0 - 0 + 
 y f() x y f () x
 g(x) 
Dựa vào bảng biến thiên , hàm số gx() có đúng 1 cực đại. Ta chon đáp án 
Bài 4. (Trích đề thi thử của trường THPT Chuyên Chu Văn An – Hà Nội – 2018 ) 
 y 
Cho hàm số . Hàm số có đồ thị 3 
 x2 
như hình vẽ bên. Hàm số y f(1 x ) x 
 2 
nghịch biến trên khoảng 
 1 3 
A. 3;1 B. 2;0 -1 O 
 3 - 3 -3/2 x 
C. 1;3 D. 1; 1 
 2
 y=f’(x) 
 - 3 
 - 5 
Gv: Phạm Xuân Hải – Trường THPT Chuyên Võ Nguyên Giáp - QB Page 9 
 RÈN LUYỆN KỸ NĂNG ĐỌC ĐỒ THỊ HÀM SỐ 2018 
Vì vậy I sai, II đúng. Ta kiểm tra tính đúng sai của III. 
Đặt SS12, lần lượt là diện tích hình phẳng được giới hạn bởi đồ thị hàm số fx () , trục Ox trên 
 23
 1;2 2;3 SS f ()() x dx f x dx ff(1) (3)
đoạn   và   . Dễ dàng có 12 nên . Suy ra . Nên III 
 12
sai. Nên ta chọn B 
III. KẾT LUẬN 
 Trên đây là một số lý thuyết và các ví dụ minh họa về vấn đề này. Hy vọng sẽ ít nhiều 
giúp ích cho các em học sinh 12 trong kỳ thi THPT sắp tới. 
Gv: Phạm Xuân Hải – Trường THPT Chuyên Võ Nguyên Giáp - QB Page 11