Tài liệu Ôn tập kiến thức môn Toán 12 - Chuyên đề: Sử dụng phương pháp tọa độ giải một số bài toán hình học không gian

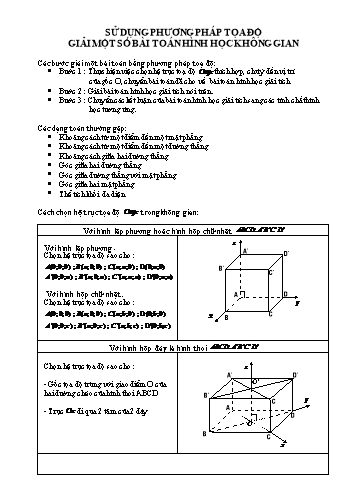
 SỬ DỤNG PHƯƠNG PHÁP TỌA ĐỘ
 GIẢI MỘT SỐ BÀI TOÁN HÌNH HỌC KHÔNG GIAN
Các bước giải một bài toán bằng phương pháp toạ độ:
 • Bước 1 : Thực hiện việc chọn hệ trục toạ độ Oxyz thích hợp, chú ý đến vị trí 
 của gốc O, chuyển bài toán đã cho về bài toán hình học giải tích
 • Bước 2 : Giải bài toán hình học giải tích nói trên. 
 • Bước 3 : Chuyển các kết luận của bài toán hình học giải tích sang các tính chất hình 
 học tương ứng.
Các dạng toán thường gặp:
 • Khoảng cách từ một điểm đến một mặt phẳng
 • Khoảng cách từ một điểm đến một đường thẳng
 • Khoảng cách giữa hai đường thẳng
 • Góc giữa hai đường thẳng
 • Góc giữa đường thẳng với mặt phẳng
 • Góc giữa hai mặt phẳng
 • Thể tích khối đa diện
Cách chọn hệ trục tọa độ Oxyz trong không gian:
 Với hình lập phương hoặc hình hộp chữ nhật ABCD.A'B'C'D'
 z
 Với hình lập phương. 
 Chọn hệ trục tọa độ sao cho : A’ D’
 A(0;0;0) ; B(a;0;0) ; C(a;a;0) ; D(0;a;0) B’
 C’
 A'(0;0;a) ; B '(a;0;a) ; C '(a;a;a) ; D'(0;a;a)
 Với hình hộp chữ nhật. A D
 Chọn hệ trục tọa độ sao cho : y
 A(0;0;0) ; B(a;0;0) ; C(a;b;0) ; D(0;b;0) 
 x B C
 A'(0;0;c) ; B '(a;0;c) ; C '(a;b;c) ; D'(0;b;c) 
 Với hình hộp đáy là hình thoi ABCD.A'B'C'D'
 Chọn hệ trục tọa độ sao cho : z
 A’ D’
 - Gốc tọa độ trùng với giao điểm O của O’
 hai đường chéo của hình thoi ABCD B’
 C y
 - Trục Oz đi qua 2 tâm của 2 đáy A
 D
 O
 B C
 x Với hình chóp S.ABC có SA  (ABC) và ABC vuông tại A
 z
Tam giác ABC vuông tại A có 
AB a; AC b đường cao bằng h . S
Chọn hệ trục tọa độ như hình vẽ sao 
cho A(0;0;0) 
 Khi đó : B a;0;0 ; C 0;b;0 y
 C
 S 0;0;h A
 B x
 Với hình chóp S.ABC có SA  (ABC) và ABC vuông tại B
Tam giác ABC vuông tại B có z
BA a; BC b đường cao bằng h . S
Chọn hệ trục tọa độ như hình vẽ sao 
cho B(0;0;0) 
 y
 Khi đó : A a;0;0 ; C 0;b;0 x
 S a;0;h
 A C
 B
 Với hình chóp S.ABC có (SAB)  (ABC), SAB cân tại S
 và ABC vuông tại C
 z
 ABC vuông tại C CA a;CB b S
chiều cao bằng h
H là trung điểm của AB y
 x
Chọn hệ trục tọa độ như hình vẽ sao 
cho C(0;0;0) A H B
Khi đó : A a;0;0 ; B 0;b;0
 C
 a b
 S( ; ;h)
 2 2 Ta có : (AB'D') : x y z 0 
 a. Tính d (AB'D'),(C'BD) (C'BD) : x y z a 0 
 Phương trình tổng quát của mặt phẳng (AB'D') // (C'BD) 
 (C'BD) (C'BD) : x y z a 0 Trong a
 d (AB'D'),(C'BD) d B,(AB'D') 
 đó vectơ pháp tuyến của mặt phẳng 3
 n C'B,C'D (a2;a2; a2 )
 (C'BD) 2   
 b. Tính cos (DA'C),(ABB' A') Vec tơ pháp tuyến của (ABB' A') là j (0 ;1; 0) 
 Oy  (ABB' A') Vec tơ pháp tuyến của 
 Vectơ pháp tuyến của (DA'C) : n3 (0;1; 1) 
 (ABB' A') là j (0 ;1; 0) 1
 Vectơ pháp tuyến của (DA'C) : cos (DA'C),(ABB' A') 
 2 
 n DA', DC (0;a2; a2 ) a2 (0;1; 1) (DA'C),(ABB' A') 45o
 3   
Bài toán 2. Cho hình lập phương ABCD.A'B'C'D'có cạnh bằng a. Tìm khoảng cách giữa hai 
đường thẳng B'D'và A'B
 Hướng dẫn Bài giải
 Chọn hệ trục toạ độ Đêcac z
 vuông góc Oxyz như sau : 
 A’
 O  A(0;0;0) ; A'(0;0;a) ; D’
 B(0;a;0) ; B'(0;a;a) B’
 C’
 C(a;a;0) ; C'(a;a;a) 
 D(a;0;0) ; D'(a;0;a) y
 A
 D
 B
 x C
  
 Tính d B'D', A'B Ta có : B'D' (a; a;0) 
   
 [B'D', A'B].BB' A' B (0;a; a) ; BB ' (0;0;a) 
 d B'D', A'B   
 2 2 2
 [B'D', A'B] B ' D ', A' B (a ; a ; a ) 
    
 3
 B ' D ', A' B .BB ' a 0
 a3 a3 a 3
 d B'D', A'B 
 a4 a4 a4 a2 3 3
Bài toán 3. Trong không gian với hệ toạ độ Oxyz cho hình chóp S.ABCD có đáy ABCD là 
hình thoi. AC cắt BD tại O. Biết SO vuông góc với (ABCD), AC=4; BD=2; SO= 2 2 . Gọi M 
là trung điểm của SC .
 a. Tính góc giữa hai đường thẳng SA và BM
 b. Tính khoảng cách giữa hai đường thẳng SA và BM Bài toán 5 . Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a . Gọi E là điểm 
đối xứng của D qua trung điểm của SA, M là trung điểm của AE, N là trung điểm của BC. 
Tính khoảng cách giữa hai đường thẳng MN và AC. 
 Hướng dẫn Bài giải
 z
 Gọi O là tâm của hình vuông 
 S
 ABCD SO  (ABCD) E
 Chọn hệ trục toạ độ Đêcac vuông 
 P
 góc Oxyz như sau : M
 O(0;0;0) ; S 0;0;h ; 
 y
 a 2 a 2 
 A ; C D
 ;0;0 ;0;0 A
 2 2 D
 a 2 a 2 
 O
 0; ;0 ; B 0; ;0 
 2 2 
 B N C x
 Toạ độ trung điểm P của SA P
   ah 2 
 a 2 h a 2 a 2 Ta có : MN, AC 0; ;0 
 ; E 2 
 ; 0 ; ; ;h 
 4 2 2 2 
  a 2 h 
 a 2 a 2 h a 2 a 2 AM 0; ; 
 M ; ; N ; ;0 4 2 
 2 4 2 4 4 
    a2 h
    a2h [MN, AC].AM
 4 a 2
 Vì : MN, AC .AM 0 d MN, AC   
 4 [MN, AC] a2 h2 4
 MN và AC chéo nhau 
 2
Bài toán 6 . Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a ; SA a ; 
SB a 3 và mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là trung 
điểm của các cạnh AB, BC . 
 a. Tính thể tích khối chóp S.BMDN
 b. Tính cosin của góc giữa hai đường thẳng SM, DN 
 Hướng dẫn Bài giải
 z
 Gọi H là hình chiếu vuông góc 
 của S trên AB SH  (ABCD) S
 Ta có : SA2 SB2 a2 3a2 AB2
 SAB vuông tại S SM a
 a 3
 Do đó : SAM đều SH 
 2
 A D
 Chọn hệ trục toạ độ Đêcac vuông y
 góc Oxyz như sau : H (0;0;0) ; S H K
 a 3 a M
 0;0; ; A ;0;0 ; B B
 2 2 x N C
 3a a 
 ;0;0 ; D ;2a;0 ; M
 2 2    a3
 Vì : AM , B 'C AB ' 
 2
 AM và B’C chéo nhau
    
 AM , B 'C AB '
 d AM , B 'C   
 AM , B 'C 
 a3
 a 7
 2 
 1 7
 2a4 a4 a4
 2
Bài toán 8. Cho hình chóp S.ABCD có đáy ABCD là hình thang , B· AD ·ABC 900 
AB BC a , AD 2a , SA vuông góc với đáy và SA 2a . Gọi M, N lần lượt là trung điểm 
của SA và SD. Tính thể tích của khối chóp S.BCNM 
 Hướng dẫn Bài giải
 z
 Chọn hệ trục toạ độ Đêcac vuông góc 
 Oxyz như sau :
 S
 A(0;0;0) ; B a;0;0 ; C a;a;0 ; D
 N
 0;2a;0 ; S 0;0;2a M
 M 0;0;a ; N 0;a;a 
 y
 A D
 B
   
 SM 0;0; a ; SC a;a; a C
   x
 SB a;0; 2a ; SN 0;a; a 
   + Tính thể tích của khối chóp S.BCNM theo a
 SM , SC a2 ; a2 ;0
 VS.BCNM VSMCB VSMCN
 1    a3
    V SM , SC SB 
 3 SMCB 
 SM , SC SB a 6 6
    1    a3
 SM , SC SN a3 V SM , SC SN 
 SMCN 6 6
 a3
 V V V đvtt
 S.BCNM SMCB SMCN 3
Bài toán 9 . Cho hình chóp S.ABCD có đáy là hình thang , ·ABC B· AD 900 AB BC a , 
AD 2a , SA vuông góc với đáy và SA a 2 . Gọi H là hình chiếu của A trên SB. Tính 
khoảng cách từ H đến mặt phẳng (SCD) 
 Hướng dẫn Bài giải