Tài liệu Ôn thi môn Toán THPTQG - Chuyên đề: Nguyên hàm. Tích phân. Ứng dụng của tích phân - Tạ Quốc Khánh

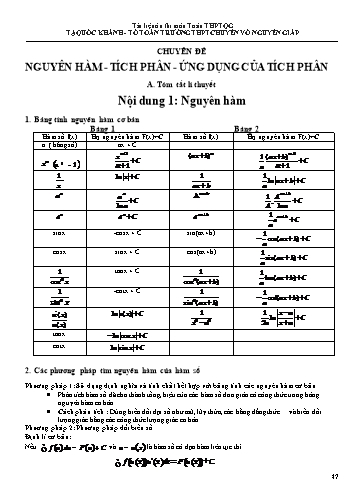
 Tài liệu ụn thi mụn Toỏn THPTQG
 TẠ QUỐC KHÁNH - TỔ TOÁN TRƯỜNG THPT CHUYấN Vế NGUYấN GIÁP
 CHUYấN ĐỀ
NGUYấN HÀM - TÍCH PHÂN - ỨNG DỤNG CỦA TÍCH PHÂN
 A. Túm tắt lớ thuyết
 Nội dung 1: Nguyờn hàm
1. Bảng tớnh nguyờn hàm cơ bản
 Bảng 1 Bảng 2
 Hàm số f(x) Họ nguyờn hàm F(x)+C Hàm số f(x) Họ nguyờn hàm F(x)+C
 a ( hằng số) ax + C
 x 1 (ax b) 1 (ax b) 1
 C C
 x (a ạ - 1) 1 a 1
 1 x C 1 1
 ln ln ax b C
 x ax b a
 ax ax Aax b 1 Aax b
 C . C
 ln a A ln a
 x x ax b 1
 e e C e eax b C
 a
 sinx -cosx + C sin(ax+b) 1
 cos(ax b) C
 a
 cosx sinx + C cos(ax+b) 1
 sin(ax b) C
 a
 1 tanx + C 1 1
 tan(ax b) C
 cos2 x cos2 (ax b) a
 1 -cotx + C 1 1
 cot(ax b) C
 sin2 x sin2 (ax b) a
 u'(x) ln u(x) C 1 1 x a
 2 2 ln C
 u(x) x a 2a x a
 tanx ln cos x C
 cotx ln sin x C
2. Cỏc phương phỏp tỡm nguyờn hàm của hàm số
Phương phỏp 1: Sử dụng định nghĩa và tớnh chất kết hợp với bảng tớnh cỏc nguyờn hàm cơ bản
 • Phõn tớch hàm số đó cho thành tổng, hiệu của cỏc hàm số đơn giản cú cụng thức trong bảng 
 nguyờn hàm cơ bản.
 • Cỏch phõn tớch : Dựng biến đổi đại số như mũ, lũy thừa, cỏc hằng đẳng thức ... và biến đổi 
 lượng giỏc bằng cỏc cụng thức lượng giỏc cơ bản.
Phương phỏp 2: Phương phỏp đổi biến số
Định lớ cơ bản:
Nếu ũ f (u)du = F (u)+ C và u = u(x) là hàm số cú đạo hàm liờn tục thỡ 
 ũ f (u(x))u '(x)dx = F (u(x))+ C 
 47 Tài liệu ụn thi mụn Toỏn THPTQG
 TẠ QUỐC KHÁNH - TỔ TOÁN TRƯỜNG THPT CHUYấN Vế NGUYấN GIÁP
 Nội dung 2: Tớnh tớch phõn
 A. Túm tắt lớ thuyết
I. CÁC PHƯƠNG PHÁP TÍNH TÍCH PHÂN
1. SỬ DỤNG ĐN VÀ CÁC TÍNH CHẤT TÍCH PHÂN
a. Định nghĩa: Cho hàm số y = f(x) liờn tục trờn K và a,b K. Giả sử F(x) là một nguyờn hàm của hàm 
 số f(x) trờn K thỡ :
 b
 b
 f (x)dx F(x) F(b) F(a) ( Cụng thức NewTon - Leipniz)
  a
 a
b. Cỏc tớnh chất của tớch phõn
 b a
 • Tớnh chất 1: f (x)dx f (x)dx
 a b
 • Tớnh chất 2: Nếu hai hàm số f(x) và g(x) liờn tục trờn a;b thỡ
 b b b
  f (x) g(x)dx f (x)dx g(x)dx
 a a a
 • Tớnh chất 3: Nếu hàm số f(x) liờn tục trờn a;b và k là một hằng số thỡ
 b b
 k. f (x)dx k. f (x)dx
 a a
 • Tớnh chất 4: Nếu hàm số f(x) liờn tục trờn a;b và c là một hằng số thỡ
 b c b
 f (x)dx f (x)dx f (x)dx
 a a c
 • Tớnh chất 5: Tớch phõn của hàm số trờn a;b cho trước khụng phụ thuộc vào biến số , 
 b b b
 nghĩa là : f (x)dx f (t)dt f (u)du ...
 a a a
2. PHƯƠNG PHÁP ĐỔI BIẾN SỐ 
 b
a) DẠNG 1: Tớnh I = f[u(x)].u' (x)dx bằng cỏch đặt t = u(x)
 a
 b u(b)
Cụng thức đổi biến số dạng 1: f u(x).u'(x)dx f (t)dt
 a u(a)
Cỏch thực hiện:
 Bước 1: Đặt t u(x) dt u ' (x)dx
 x b t u(b)
 Bước 2: Đổi cận : 
 x a t u(a)
 Bước 3: Chuyển tớch phõn đó cho sang tớch phõn theo biến t ta được
 b u(b)
 I f u(x).u'(x)dx f (t)dt (tiếp tục tớnh tớch phõn mới)
 a u(a)
 49 Tài liệu ụn thi mụn Toỏn THPTQG
 TẠ QUỐC KHÁNH - TỔ TOÁN TRƯỜNG THPT CHUYấN Vế NGUYấN GIÁP
II. CÁC VÍ DỤ
 2 x2 + 3x + 1
Vớ dụ 1: Tớnh tớch phõn I = dx . (Phõn tớch & dựng định nghĩa)
 ũ x2 + x
 1
Bài giải
 x2 + 3x + 1 2x + 1
♥ Biến đổi hàm số thành dạng = 1+
 x2 + x x2 + x
 2 x2 + 3x + 1 2 2 2x + 1
 Khi đú: I = dx = dx + dx
 ũ x2 + x ũ ũ x2 + x
 1 1 1
 2
 2
 ã dx = x = 1 
 ũ 1
 1
 2
 2x + 1 2
 ã dx = ln x2 + x = ln 3 
 ũ x2 + x 1
 1
♥ Vậy I = 1+ ln 3. 
 1 (x + 1)2
Vớ dụ 2: Tớnh tớch phõn I = dx . (Phõn tớch & dựng định nghĩa)
 ũ x2 + 1
 0
Bài giải
 2
 (x + 1) x2 + 2x + 1 2x
♥ Biến đổi hàm số thành dạng = = 1+ 
 x2 + 1 x2 + 1 x2 + 1
 2
 1 (x + 1) 1 1 2x
 Khi đú: I = dx = dx + dx
 ũ x2 + 1 ũ ũ x2 + 1
 0 0 0
 1
 1
 ã dx = x = 1 
 ũ 0
 0
 1
 2x 1
 ã dx = ln x2 + 1 = ln 2 
 ũ x2 + 1 0
 0
♥ Vậy I = 1+ ln 2 . 
 ln 2
 2
Vớ dụ 3: Tớnh tớch phõn I = ũ(ex - 1) exdx . (Đổi biến số dạng 1)
 0
Bài giải
♥ Đặt t = ex - 1ị dt = exdx 
 51 Tài liệu ụn thi mụn Toỏn THPTQG
 TẠ QUỐC KHÁNH - TỔ TOÁN TRƯỜNG THPT CHUYấN Vế NGUYấN GIÁP
Bài giải
 ùỡ du = dx
 ùỡ u = x + 1 ù
♥ Đặt ớ ị ớ 1 
 ợù dv = sin 2xdx ù v = - cos 2x
 ợù 2
 p p
 1 4 1 4
 Suy ra: I = - (x + 1)cos 2x + sin 2x 
 2 0 4 0
 p p
 1 4 1 4 3
 = - (x + 1)cos 2x + sin 2x = 
 2 0 4 0 4
 3
♥ Vậy I = . 
 4
 p
 4
Vớ dụ 7: Tớnh tớch phõn I = ũ x(1+ sin 2x)dx . (Tớch phõn từng phần)
 0
 p p p p p
 4 4 x2 4 4 p2 4
♥ Ta cú: I = xdx + xsin 2xdx = + xsin 2xdx = + xsin 2xdx 
 ũ ũ 2 ũ 32 ũ
 0 0 0 0 0
 ùỡ du = dx
 ùỡ u = x ù
 Đặt ớ ị ớ 1 
 ợù dv = sin 2xdx ù v = - cos 2x
 ợù 2
 p p p
 p p
 4 4 4
 1 4 1 1 1 4 1
 Suy ra: xsin 2xdx = - x cos 2x + cos 2xdx = cos 2xdx = sin 2x = 
 ũ 2 2 ũ 2 ũ 4 4
 0 0 0 0 0
 p2 1
♥ Vậy I = + . 
 32 4
 2 x2 + 2ln x
Vớ dụ 8: Tớnh tớch phõn I = dx . (Phõn tớch + đổi biến số dạng 1)
 ũ x
 1
Bài giải
 2 2 ln x
♥ Ta cú: I = xdx + 2 dx 
 ũ ũ x
 1 1
 2
 2 x2 3
 ã xdx = = 
 ũ 2 2
 0 1
 53 Tài liệu ụn thi mụn Toỏn THPTQG
 TẠ QUỐC KHÁNH - TỔ TOÁN TRƯỜNG THPT CHUYấN Vế NGUYấN GIÁP
 x 1 1 x x 1
 Suy ra: I2 = xe e dx = e e = 1. 
 0 0 0
♥ Vậy I = e – 1 + 1 = e. 
 B. Bài tập
Bài 1: Tớnh cỏc tớch phõn sau
 1 x 2 sin x
 1) I 2 dx 2) I 2 dx
 2 
 0 x 4 0 1 cos x 
Bài 2: Tớnh cỏc tớch phõn sau
 3
 e ln x 1 e ln3 x 2
 1) I dx 2) I dx
 1 x 1 x
Bài 3: Tớnh cỏc tớch phõn sau
 2
 1) I sin3 x cos xdx 2) I sin 2x(1 sin2 x)3dx
 0 0
Bài 4: Tớnh cỏc tớch phõn sau
 2 2 x2
 1) I x x2 3dx 2) I dx
 3
 1 0 x 1
Bài 5: Tớnh cỏc tớch phõn sau
 1 e 3
 2 ln x 
 1) I x x ex dx 2) I x 1 dx
 2 
 0 1 x 
Bài 6: Tớnh cỏc tớch phõn sau
 e 1 3ln x ln x ln3 ex
 1) I dx 2) I dx
 3
 x x
 1 0 e 1 
Bài 7: Tớnh cỏc tớch phõn sau
 2 sin2x cos x 6 tan4 x
 1) I dx 2) I dx
 0 1 cos x 0 cos 2x
Bài 8: Tớnh cỏc tớch phõn sau
 2 sin2x sin x 2 sin 2x
 1) I dx 2) I dx
 2 2
 0 1 3cos x 0 cos x 4sin x
Bài 9: Tớnh cỏc tớch phõn sau
 55